Perceptron

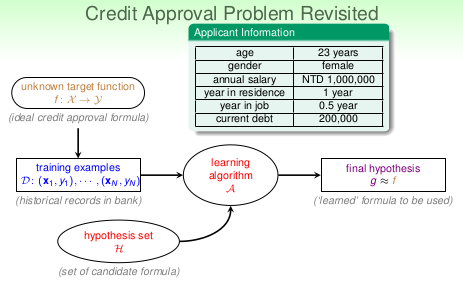
1. 之前已经了解到，机器学习的过程是：

• 输入一笔数据，这笔数据由\(\mathcal X\)和\(\mathcal Y\)组成，而x和y服从一个未知的分布\(\mathcal f\)
  
• 通过learning algorithm \(\mathcal A\)在hypothesis set \(\mathcal H\)中挑选一个合适的g，这个g即是机器学习到的，希望这个g能够很接近f，以至于能替代它。

1. 机器学习的模型是由Learning algorithm \(\mathcal A\)和 hypothesis \(\mathcal H\)组成

今天就要学习一个模型，既然是模型，学完后就要清楚地知道它的hypothesis set 和 learning algorithm

1.Perceptron Hypothesis set

1.1抽象解释

• 情景：如上图所示，已经了解客户的年龄，工资，工作年限，负债情况等，达到银行的标准，则通过他的信用卡申请。那么如果让机器来做，它要做的是什么呢？
  > 回顾机器学习的过程，我们需要有输入数据D(x,y)，Hypothesis \(\mathcal H\), learning algorithm \(\mathcal A\)。那么一一与这个情景对应，应是怎么样呢？
• 机器：
  • 把每个申请者当做一个向量\(\mathcal X\)，把申请者的信息当做不同维度的特征，则\(\mathcal X = (x_1, x_2, x_3,\dots, x_n)\)
  • 把同意申请设为\(+1\)，不同意申请设为\(-1\), 则\(\mathcal Y: \{+1(good), -1(bad)\}, 0 忽略\)
  • 银行的标准即为阈值（threshold）
  • 不同维度的特征应该有不一样的权重\(\mathcal w\)

那么 \[ \mathcal H: h(x) = sign((\sum_{i=1} ^n w_i x_i) - threshold) \]

这个式子可以做一个数学上的简化： \[ \begin{aligned} h(x) &= sign((\sum_{i=1} ^n w_i x_i) - threshold)\\ &= sign((\sum_{i=1} ^n w_i x_i) +(- threshold) \cdot (+1))\\ &= sign(\sum_{i=0} ^n w_i x_i)\\ &= sign(\mathbf w^\mathrm{T} \mathbf x) \end{aligned} \]

这里将$ -threshold$ 当作\(w_0, 1当作x_0\), 从而将式子整理为两个向量内积的形式

1.2图像意义

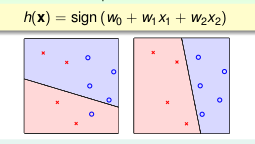
上图是perceptron在二维平面上的展示。

• \(\mathrm x\) 代表平面上的一个点，每个特征代表一个维度，这个图中只有两个特征
• \(\circ\) 代表\(+1\), \(\times\) 代表\(-1\)
• 直线代表\(\mathrm{h}\)

因此，正的应该在一边，负的应该在另一边 所以，二维的perceptron就是一个线性分类器，当然，可以想象，三维的perceptron也是一个分类器，不过不在是一条线，而是一个面

2.Perceptron Learning Algorithm

前面已经说了一个模型是由Hypothesis set和Learning Algorithm组成，光知道Hypothesis set是不够的，还需要知道如何从hypothesis set中选取一个合适的g，使\(g \approx f\)，而这个过程就是learning algorithm所做的。

1. 我们的目的是得到一个g，并且\(g \approx f\)，但我们怎么判断g和f很接近呢？

• 我们知道的就是\(\mathbf{X}\)和\(\mathcal{y}\)，所以如果\(g \approx f\)就会有\(g(\mathbf{x_n}) = f(\mathbf{x_n}) = \mathcal{y_n}\)

1. 但hypothesis set中有无数条线，怎么办呢？

• 可以想像最开始有一条线，当这条线有错误时，就去修正它，直至它没出错为止

1. 如何修正呢？

• 一轮一轮的修正。\(t=0,1,2\dots\)代表在第几轮, 若第t轮中，在一个点上\((\mathbf{x_{n(t)}},{y_{n(t)}})\)使得\(sign(\mathbf{w_{t}^\mathrm{T}}\mathbf{x_{n(t)}}) \neq {y_{n(t)}}\),则令\(\mathbf{w_{t+1}} = \mathbf{w_{t}} + \mathrm{y_{n(t)}}\mathbf{x_{n(t)}}\)，直到没有错误。然后将\(\mathbf{w}\)返回，当作g

1. 怎么判断它没有错误了呢？

• 将这些点编号，在每一轮中，按顺序去一个点一个点的检查，或者随机不重复的检查，当这些点全都遍历完，且没有错误的点，则没有错误了

按以上这种方式进行，称为cycle PLA

但依然有些疑问：

• 这样做PLA是否一定会停下来呢？
• 即使停下来，$ $
• 在样本以外的数据上表现怎么样呢？
• 如果不会停呢？

3.Guarantee of PLA

如果PLA能够停下来，那么所有的点肯定被分成了两部分，即数据被分成了两部分。那么这部分数据就是线性可分（linear separatablility的。反过来，由数据是线性可分一定能推出PLA可以停下来吗？

数据是线性可分，代表存在一条线，可以将数据分成两部分（如下图所示），不妨将这条线表示为\(w_f\)，既然将数据分成了两部分肯定有 \[ \min_{n}y_{n}w_{f}^\mathrm{T}x_{n} > 0 \] \(y_{n}w_{f}^\mathrm{T}x_{n}\)表示的是点到直线的距离。也肯定有 \[ y_{n(t)} \mathbf{w}_{f}^\mathrm{T} \mathbf{x_{n(t)}} > \min_{n}y_{n}w_{f}^\mathrm{T}x_{n} > 0 \]

每次更新的过程： \[ \begin{aligned} \mathbf{w}_{f}^\mathrm{T}\mathbf{w}_{t} &= \mathbf{w}_{f}^\mathrm{T}(\mathbf{w}_{t-1} + y_{n(t-1)}\mathbf{x_{n(t-1)}})\\ & \ge \mathbf{w}_{f}^\mathrm{T}\mathbf{w}_{t-1} + \min_{n}y_{n}w_{f}^\mathrm{T}x_{n}\\ & \ge \mathbf{w}_{f}^\mathrm{T}\mathbf{w}_{t-2} + 2\min_{n}y_{n}w_{f}^\mathrm{T}x_{n}\\ & \ge \mathbf{w}_{f}^\mathrm{T}\mathbf{w}_{t-3} + 3\min_{n}y_{n}w_{f}^\mathrm{T}x_{n}\\ & \vdots \\ & \ge \mathbf{w}_{f}^\mathrm{T}\mathbf{w}_{0} + t\min_{n}y_{n}w_{f}^\mathrm{T}x_{n} \end{aligned} \]

\(w_{0} = 0\)，所以

\[ \mathbf{w}_{f}^\mathrm{T}\mathbf{w}_{t} \ge t\min_{n}y_{n}w_{f}^\mathrm{T}x_{n}\\ \]

根据上式，可以看出\(w_f\)和\(w_t\)的内积的确越来越大，但是不一定是越来越靠近，可能只是\(||w_t||\)变大了

同时，当\(sign(\mathbf{w}_t^{\mathrm{T}} \mathbf{x}_{n(t)}) \neq y_{n(t)}\)时，\(w_t\)会改变。易得\(y_{n(t)} \mathbf{w}_t^\mathrm{T} \mathbf{x}_{n(t)} \le 0 \Leftrightarrow sign(\mathbf{w}_t^{\mathrm{T}} \mathbf{x}_{n(t)}) \neq y_{n(t)}\)

\[ \begin{aligned} ||\mathbf{w}_{t}||^2 & = ||\mathbf{w_{t-1}} + y_{n(t-1)}\mathbf{x}_{n(t-1)}||^2\\ & = ||\mathbf{w_{t-1}}||^2 + 2y_{n(t-1)} \mathbf{w}_t^{\mathrm{T}} \mathbf{x}_{n(t-1)} + ||y_{n(t-1)} \mathbf{x}_{n(t-1)}||^2\\ & \le ||\mathbf{w_{t-1}}||^2 + 0 + ||y_{n(t-1)} \mathbf{x}_{n(t-1)}||^2\\ & \le ||\mathbf{w_{t-1}}||^2 + \max_n||y_{n} \mathbf{x}_{n}||^2\\ & \le ||\mathbf{w_{t-2}}||^2 + 2\max_n||y_{n} \mathbf{x}_{n}||^2\\ & \vdots \\ & \le ||\mathbf{w_{0}}||^2 + t\max_n||y_{n} \mathbf{x}_{n}||^2\\ & \le t\max_n||y_{n} \mathbf{x}_{n}||^2 \end{aligned} \]

\[ \begin{aligned} \dfrac{\mathbf{w}_f^{\mathrm{T}}}{||\mathbf{w}_f||} \dfrac{\mathbf{w}_T}{||\mathbf{w}_T||} &\ge \dfrac{t\min \limits_n y_{n}w_{f}^\mathrm{T}x_{n}}{||w_f||\sqrt{t\max \limits_n||y_{n} \mathbf{x}_{n}||^2}}\\ &\ge \sqrt{t}\dfrac{\min \limits_n y_{n} \dfrac{w_{f}^\mathrm{T}}{||w_f||}x_{n}} {\max \limits_n||y_{n} \mathbf{x}_{n}||}\\ &= \sqrt{t}\dfrac{\min \limits_n y_{n} \dfrac{w_{f}^\mathrm{T}}{||w_f||}x_{n}} {\max \limits_n|| \mathbf{x}_{n}||} \end{aligned} \]

由此可以看出，\(w_f\)和\(w_T\)确实越来越靠近,最终重合，所以 \[ \dfrac{\mathbf{w}_f^{\mathrm{T}}}{||\mathbf{w}_f||} \dfrac{\mathbf{w}_T}{||\mathbf{w}_T||} \le 1 \] 令$ = _n ||x_n||^2= _n y_n _n $

\[ \sqrt{t}\dfrac{\min \limits_n y_{n} \dfrac{w_{f}^\mathrm{T}}{||w_f||}x_{n}} {\max \limits_n|| \mathbf{x}_{n}||} \le 1\\ t \le \dfrac{\mathrm{R^2}}{\rho ^2} \]

可以看出t是有上界的，所以当数据是线性可分的时候，PLA最终会停

4.Non-Separable Data

经过以上的推理，可以知道，当\(\mathcal{D}\) 是线性可分的时候，PLA 会选取的线会越来越接近\(w_f\)并最终停止。来总结下PLA算法的优缺点

• pros
  • 实现简单，可以用于任何维度
• cons
  • 需要假定\(\mathcal{D}\)是线性可分的
  • 不能确定多久才能停？（不停可能是还没跑完，也可能是\(\mathcal{D}\)根本不是线性可分的）

所以，如果\(\mathcal{D}\)不是线性可分怎么办呢？

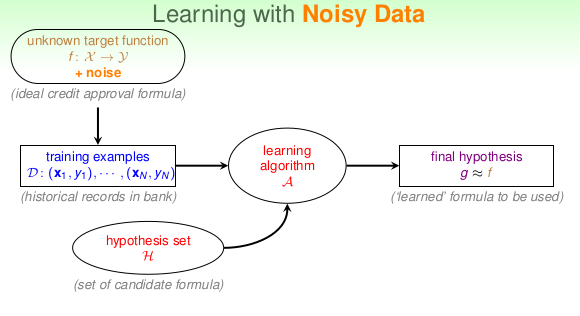
首先机器学习的\(\mathcal{D}\)的设定并不是完全基于target function \(f\)，可能在收集数据或者产生数据的时候就有噪声，在这样的情况下，如何找到一个g并且\(g \approx f\)?

一般情况下，噪声不会太多，因此，通常情况下，\(y_n = f(x_n)\)，那么也可以找到一个g且\(g \approx f on \mathcal{D}\)，也即通常情况下，\(y_n = g(x_n)\)

既然这样，能否像这样找出g呢？

\[ \mathbf{w}_g \leftarrow \mathop{\arg\max}_\mathbf{w}\sum_{n=1}^N\parallel y_n \neq sign(\mathbf{w}^\mathrm{T}\mathbf{x}_n) \parallel \]

这样做是不可能的.NP-hard

能否通过修改之前的PLA，然后来找出g呢？ 这个是可以的，很容易想到，噪声并不算多，找一个犯错犯的少的线即可。这种PLA称作pocket PLA。其原理和贪心法很像。

1. 初始化\(\mathbf{w}\)
2. 随机找一个点，看是否有错
3. 若有错，则更正这个错误,\(w_{t+1} \leftarrow w_t + y_{n(t)}x_{n(t)}\)
4. 如果\(w_{t+1}\)这条线犯的错误更少，则替换\(\hat{\mathcal{w}}\)
5. 重复第2,3,4步操作
6. 经过足够多轮的迭代后，返回\(\hat{\mathcal{w}}\)